|
|
Rekursion er et ord der kan få det til at løbe koldt
ned af ryggen på de fleste begyndere inden for programmering, men når
man først mestrer rekursionens enkelthed og styrke, vil man aldrig ønske
at undvære den igen.
|
| Nedbrydning
|
Lad os som udgangspunkt se på en af de vigtigste teknikker
i algoritmekonstruktion, nemlig nedbrydning. Algoritmisk set tager man
et problem, deler det i mindre dele og nedbryder dem igen, indtil problemet
umiddelbart kan løses af den der skal gøre det, f.eks. en computer.
Når vi nedbryder, søger vi ofte at dele problemet i to nogenlunde lige
store dele. Dermed opnår vi nemlig, at vi ikke skal fortsætte nedbrydningen
i så lang tid; vores dele bliver hurtigere mindre.
|
| Samme slags problem
|
Hvad hvis vi gik i den helt anden grøft, og nedbrød
ved kun at løse en så simpel del af problemet, at det umiddelbart kunne
løses af den der skal udføre det? I den situation vil det resterende
problem kun være blevet lidt mindre. En sådan fremgangsmåde vil kun
være interessant hvis vi derved kom til at stå med et lidt mindre problem
der var at samme slags som det vi først havde - men altså lidt mindre!
|
|
|
Hvis man gjorde selve den proces vi udførte ved at
nedbryde, til en del at algoritmen; havde vi dermed lavet en algoritme
der kunne løse det samlede problem. Når computeren kommer og beder om
nye instrukser, kan vi sige: "Gør det samme som før: tage en lille
del fra, som du kan løse, og lad resten være". Når den så kommer
med det endnu mindre problem vil den få samme besked, indtil den kommer
med et problem der er så lille at den umiddelbart kan løse det.
|
| Rekursion vs. Iteration
|
Tanken kunne her godt falde på iteration, gentagelse.
Rekursion og iteration er på sin vis også to konkurrerende begreber
i programmering, man kan lave rekursion om til iteration. Hvilken løsning
man vælger er et praktisk spørgsmål. I en konkret situation kan den
ene løsning være besværlig at konstruere, mens den anden er ligetil.
|
|
|
Rekursion er nok det mest specielle algoritmiske begreb
der findes. Der er nogle der mener det er overflødigt, der er andre
der mener det er evig saliggørende. Der er dem der mener det er svært,
der er igen andre der mener det er let. En ting er de fleste dog enige
om: Det er interessant!
|
| Rekursion er når man kalder sig selv
| Rekursion er når en metode kalder sig selv. Man taler om
at "metoden er rekursiv". Man kan også sige at en definition
er rekursiv; hvis den definerer noget ved sig selv. Som vi senere skal
se er der ofte en tæt sammenhæng mellem en rekursiv definition og en rekursiv
metode.
|
|
|
1. Ikast Svømmehal
|
|
|
Rekursion er grundlæggende et meget abstrakt begreb.
Når man derfor skal illustrere hvor det kan anvendes uden at det bliver
for kompliceret fra starten, må man vælge eksempler, der ofte virker
som taget ud af en absurd virkelighed, og eksemplet med Ikast svømmehal
er ingen undtagelse.
|
| Er der nogen røde bolde?
|
Af uransagelige grunde har man tømt bassinet for vand
og i stedet fyldt det med bordtennisbolde. Alle bordtennisboldene er
hvide, men i nattens løb har der været ubudne gæster. Man kan derfor
ikke længere med sikkerhed sige at bassinet kun indeholder hvide bolde,
da man på den ubudne gæsts bopæl fandt op til flere røde bolde. Om han
har nået at smide nogle røde bolde i bassinet, før han blev pågrebet
vides ikke. Hvordan skal man undersøge om alle boldene er hvide? Man
kunne skue ud over bassinet, mens andre rørte rundt i det, og håbe at
eventuelle røde bolde ville vise sig. Ikke nogen sikker metode! Da vi
arbejder med computere og alt dette vrøvl til slut ender som kode, kan
vi se bort fra hvor lang tid vores algoritme vil tage, når den udføres
manuelt. Vi kunne derfor løse problemet ved at tage en bold
op af gangen, undersøge den, lægge den til side, tage en bold op af
bassinet osv. indtil der ikke var flere bolde i bassinet.
|
|
|
Den måde vi løser problemet på er nedbrydning. Der
er dog en "ny ting" der er værd at bemærke. Hver gang vi løser
en del af problemet har vi en del tilbage, der er af nøjagtig samme
slags som det vi startede med, men det er blevet "mindre".
Vi kan altså ved en gentagelse arbejde os ind på problemet og til sidst
løse det. En metode man kunne kalde salami-metoden.
|
|
|
Vi kan løseligt beskrive vores algoritme rekursivt ved:
|
Pseudo 1:
Check af bassin
|
void checkBassin( Bassin b ) {
checkEnBold( b );
if ( !tom( b ) )
checkBassin( b );
} |
|
| Uafhængige metode-kopier
|
Man observerer at
checkBassin() kaldes
rekursivt, den kalder sig selv! Det ser på denne måde ud som en løkke,
hvor kaldet er et slags spring tilbage.
Sådan skal det kun i meget ringe grad forstås. Når metoden kaldes
rekursivt er det ikke den samme metode der køres igen, det er helt igennem
en kopi! Hvis den havde haft nogen lokale
variable ville de, selvom de havde samme navn som de andre kopier af
checkBassin() være
100% uafhængige af hinanden. Når checkBassin() bruger dem, vil det ingen betydning have for de "samme" lokale
variable som de andre kopier har.
|
|
| Begrebet rekursion stammer i første række fra matematisk rekursive definitioner,
og de mest simple eksempler på rekusion er da også matematiske.
|
|
|
2. Matematiske eksempler
|
|
|
2.1 Fakultet
|
|
|
Fakultet funktionen N! beregnes ved at gange N med N-1, N-2, osv. ned
til 1. Lad os se et eksempel med 5!
|
|
|
| 5! = 5 * 4 * 3 * 2 * 1 = 120 |
|
|
|
Man ganger altså elementerne i en talrække for at få resultatet.
|
|
|
Hvis man indsætter en parantes i beregningen af 5! vil man se at det
kan skrives som 5 gange 4!
|
|
|
|
5! = 5 * 4 * 3 * 2 * 1 = 5 * ( 4 * 3 * 2 * 1 ) = 5 * 4!
idet 4! = 4 * 3 * 2 * 1 |
|
|
|
Hvad kan man så bruge det til?
|
|
|
Man kan på den måde definere fakultet rekursivt:
|
|
|
|
|
|
som man ser, optræder ! nu på begge sider.
|
| Rekusions-skridt
| Nu kunne man måske mene at det var lidt ubehjælpsomt at definere noget
ved hjælp af sig selv. For hvor langt er man egentlig kommet ved det?
Det er rigtigt at en definition, der på denne måde bider sig selv i halen,
er i fare for ikke at være noget bevendt. Vi ønskede at vide hvad fakultet
var, og definitionen siger umiddelbart blot at fakultet er fakultet! Der
er dog et lille men, og det ligger i at vi faktisk kommer ud af stedet.
Det skyldes at det tal vi nu skal tage fakultet af (N-1) er mindre end
det oprindelige tal N. På den måde arbejder vi os nedad mod 1, hvor vi
stopper. De skridt vi tager nedad mod 1, kaldes generelt for rekursions-skridt.
|
| Rekursions-basis
| Den rolle 1 spiller i forbindelse med beregning af fakultet, at den
er en slags stopklods, har også en særlig betegnelse: Rekusions-basis,
eller i daglig tale: basis. Uden en basis vil rekursionen
aldrig stoppe, og man ville derfor opleve et fænomen ækvivalent med uendelige
løkker.
|
|
|
Man samler rekursionsskridt og basis i det der bliver den endelige
rekursive definition af fakultet:
|
|
|
|
|
|
Det bemærkes at denne basis bevirker, at man kommer til at gange 1
med sig selv. Ikke specielt effektivt, men vi vil dog alligevel holde
os til den matematiske definition i det følgende:
|
|
|
| 5! = 5 * 4 * 3 * 2 * 1 * 1 = 120 |
|
| Funktionelt orienteret notation
|
Det var så den matematisk rekursive definition; hvad med en rekursiv
metode? Den rekursive metode er i virkeligheden meget mekanisk at lave
ud fra den matematiske. Vi indfører i første omgang en funktionelt orienteret
notation og kalder N! for fak( N ):
|
|
|
|
fak( N ) = N * fak( N-1 )
fak( 0 ) = 1 |
|
|
|
Dernæst observerer vi at der er tale om selektion mht. hvilken af de
to del-definitioner vi skal bruge. Er N = 0 skal vi bruge den nederste,
ellers den øverste. Vores første udkast til en metode vil derfor være:
|
Pseudo 2:
Fakultet
|
// PRE: n >= 0
int fak( int n ) {
if ( n == 0 )
// 0! = 1
else
// N! = N * fak( N-1 )
} |
|
|
|
Her er definitionerne indsat i if-sætningen. Den endelige metode er
triviel at færdiggøre:
|
Source 1:
Rekursiv: Fakultet
|
// PRE: n >= 0
int fak( int n ) {
if ( n == 0 )
return 1;
else
return n * fak( n-1 );
} |
|
|
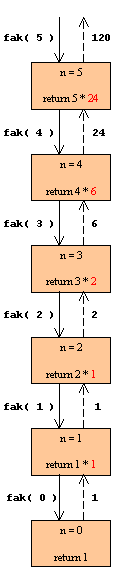
| Når man præcist vil forstå hvordan rekusionen virker, kan man lave
et diagram der beskriver forløbet for et kald, med aktuelle parametre.
Hvis vi f.eks. ser på et kald med 5,
vil vi få følgende rekursive forløb:
|
Figur 1:
Forløbet af de rekursive kald
|
|
|
| Hvert felt repræsenterer en metode-kopi. Disse kopier er, som alle
metode-kopier, uafhængige af hinanden idet deres parametre n er lokale
i hver metode-kopi; hvor de intet kender til hinandens eksistens.
|
|
| Det første kald fak( 5 )
kommer ind fra oven, og n
får værdien 5. Da n
ikke er 0 kaldes der
videre med n-1, som er
4, altså fak(
4 ).
|
|
| Sådan forløber det nedad, indtil vil kalder med 0.
Ved fak( 0 ) er n
netop 0 og der returneres
1. Returpilene er stiplede,
og man ser hvorledes delresultaterne returneres op igennem metode-kopierne
og løbende sammenregnes til det endelige resultat: 120.
|
|
| Bemærk at hver gang der returneres, slettes metode-kopien der returnerer.
Dvs. når en stiplet pil effektueres forsvinder feltet nedenunder.
|
|
| Bemærk ligeledes at vi, når vi returnerer 120,
ikke ved hvad der sker med denne værdi. Den der oprindelig kaldte med
fak( 5 ) kunne f.eks.
også være en metode-kopi af fak,
der selv var blevet kaldt med den aktuelle parameter 6.
|
|
|
Det var så en rekusiv metode, men er det noget bevendt at lave en rekursiv
frem for en iterativ løsning? Lad os betragte en iterativ metode, der
ligeledes beregner fakultet:
|
Source 2:
Iterativ: Fakultet
|
// PRE: n >= 0
int fak( int n ) {
int fakultet = 1;
for ( int faktor=n; faktor>0; faktor-- )
fakultet *= faktor;
return fakultet;
} |
|
| Ikke den store forskel
|
Man ser her at den iterative metode kræver en lokal variabel, samt
at vi ikke længere kan returnere direkte i beregningsudtrykket fordi
det gentages. Når man skal illustrere fordelen ved rekusion, gør man
det ved at sammenligne en rekursiv med en iterativ løsning, men i tilfældet
med fakultet er der ikke rigtig nogen gevinst. Grunden til at de to
metoder ser nogenlunde lige bekvemme ud, skal findes i den meget nære
sammenhæng der er mellem de talværdier vi arbejder med, og dem en for-løkke
naturligt vil gennemløbe.
|
|
|
2.2 Fibonacci
|
|
|
Fibonacci talrækken:
|
|
|
| 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... |
|
|
|
er klassisk i rekursiv sammenhæng.
|
| Leonardi Pisano
|
Leonardo Pisano (kaldet Fibonacci: "søn af Bonacci") var
den nok største europæiske matematiker i middelalderen. Han studerede
bla. al-Khwarizmi's værker ("hr. Algoritme" fra kapitlet om algoritmer).
Talrækken der er opkaldt efter ham, stammer fra et populotions problem
han opstillede: "Hvor mange kaninpar bliver det til i løbet af
et år; hvis man starter med ét kaninpar. Når der gælder at et kaninpar
føder endnu et kaninpar hver måned og det ligeledes tager en måned for
at kaninpar at blive kønsmodent". Vi skal ikke her fordybe os i
problemet, men blot notere os den historiske sammenhæng.
|
|
| Eftersom der er tale om en talrække og ikke nogen sammenregning af
tallene, er det et spørgsmål om hvilket tal der skal stå på en given position.
Sammenhængen er rekursiv, idet ethvert tal i talrækken er lig summen af
de to foregående. Dette er rekursionsskridtet.
|
|
| For de to første tals vedkommende findes der naturligvis ikke to foregående
tal. 0 og 1 er derfor givet pr. definition. De er basis.
|
|
|
Vi fastlægger dernæst at det første tal er det 0'te fibonacci-tal,
det andet er det 1'te fibonacci-tal osv. Vi indfører den notation at
Fn er det n'te fibonacci-tal.
|
|
|
Efter nu at have fastlagt notationen, kan vi formulere den rekursive
definition på fibonacci talrækken:
|
|
|
|
Fn = Fn-1 + Fn-2
F0 = 0 og F1 = 1 |
|
|
|
Dernæst skal vi formulere definitionen funktions-orienteret:
|
|
|
|
fib( n ) = fib( n-1 ) + fib( n-2 )
fib( 0 ) = 0 og fib( 1 ) = 1 |
|
|
|
Og kan endelig lave omformningen til rekursiv metode:
|
Source 3:
Rekursiv: Fibonacci
|
// PRE: n >= 0
int fib( int n ) {
if ( n < 2 )
return n;
else
return fib( n-1 ) + fib( n-2 );
} |
|
|
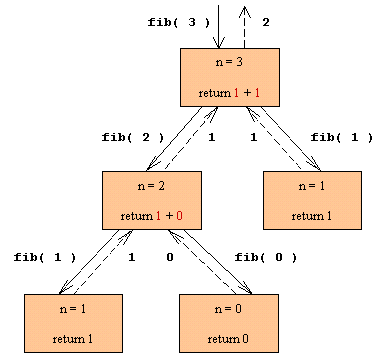
| Her foretages der to rekursive kald hver gang metoden endnu ikke har
nået basis. Derfor får diagrammet, der viser forløbet ved de rekusive
kald, en anden struktur. Lad os se det med et kald: fib(
3 ):
|
Figur 2:
Forløbet af de rekursive kald
|
|
|
| Der er nu to metode-kopier under hver af dem, pånær dem der har nået
basis. I diagrammet er det altid den venstre der kaldes først. Det betyder
i vores eksempel, at kaldet fib( 1 )
længst til højre er det sidste der bliver udført.
|
|
| Først kommer fib( 3 )
ind fra oven. Det resulterer først i et kald til venstre fib(
2 ). Dernæst kaldet fib(
1 ) ned til venstre efterfulgt af fib(
0 ) til højre. Der returneres videre op til den øverste
metode-kopi, der afslutter med kaldet fib(
1 ) yderst til højre.
|
| Spild af metode-kald
| Man bemærker at kaldet fib( 1 )
foretages to forskellige steder (der naturligvis intet kender til hinanden,
og de to metode-kopier eksisterer forøvrigt heller ikke på samme tid).
Det er på sin vis spild at det skal gøres to gange. Hvis man gjorde eksemplet
større, f.eks. fib( 20 ),
ville det være endnu mere graverende. Vi vil i opgaverne studere dette
fænomen nærmere.
|
|
|
Lad os se en iterativ metode, der finder det n'te fibonacci-tal:
|
Source 4:
Iterativ: Fibonacci
|
// PRE: n >= 0
int fib( int n ) {
if ( n < 2 )
return n;
else {
int fib2=0;
int fib1=1;
for ( int i=1; i<n ; i++ ) {
tmp = fib1;
fib1 = fib1 + fib2;
fib2 = tmp;
}
return fib1;
}
} |
|
|
| fib1 er Fn-1,
mens fib2 er Fn-2.
|
|
|
Her synes den iterative løsning mere utilgængelig end den enkle rekursive.
|
| Ny basis
|
Det skal dog retfærdigvis siges at man kan optimere den iterative løsning
lidt. Man kan nemlig foretage en udvidelse af fibonacci-tallene så også
det 0'te og det 1'te kan beregnes. Det gøres ved at starte med 1 og
0 som en slags intern forskudt basis:
|
|
|
|
1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ... |
|
|
|
Den optimerede metode bliver:
|
Source 5:
Optimeret iterativ: Fibonacci
|
// PRE: n >= 0
int fib( int n ) {
int fib2=1;
int fib1=0;
for ( int i=0; i<n ; i++ ) {
tmp = fib1;
fib1 = fib1 + fib2;
fib2 = tmp;
}
return fib1;
} |
|
|
|
Det virker, men vi skal gøres os en del krumsping, der er afhængige
af matematikken, for at opnå en nogenlunde enkel iterativ løsning.
|
|
|
2.3 Største fælles divisor
|
| Euclid
| Euclid (300 fvt.) er ophavsmand til en meget kraftfuld algoritme til
at finde den største fælles divisor (det største tal der går op i dem
begge). Metoden er rekusiv og er givet ved:
|
|
|
|
gcd( m, n ) = gcd( n, m modulus n ), hvis n ikke går op i m
gcd( m, n ) = n, ellers |
|
|
| hvor man antager: m >= n > 0. Man navngiver traditionelt funktionen,
der beregner største fælles divisor: gcd (greatest
common divider).
|
|
| Basis er, når n går op i m; hvor resultatet blot er n. Rekursions-skridtet
er et enkelt kald videre. Man bemærker at der om m modulus n
gælder: n > m modulus n > 0. Derfor passer antagelsen
om m >= n > 0 også i kaldet videre.
|
|
| Den rekusive metode bliver:
|
Source 6:
Rekursiv: Største fælles divisor
|
// PRE: m >= n > 0
int gcd( int m, int n ) {
if ( m%n == 0 )
return n;
else
return gcd( n, m%n );
} |
|
|
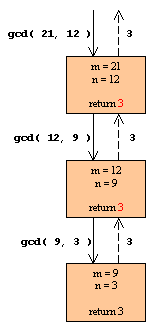
| Lad os igen tegne et diagram der viser de rekursive kalds sammenhæng.
Vi vil finde den største fælles divisor for 21 og 12:
|
Figur 3:
Forløbet af de rekursive kald
|
|
|
| Diagrammet ligner i sin struktur det vi tegnede for fakultet. Det skyldes
at de begge arbejder med ét rekursivt kald videre, mens f.eks. fibonacci
bruger to kald og dermed får en anderledes struktur.
|
|
| Den iterative løsning bliver:
|
Source 7:
Iterativ: Største fælles divisor
|
// PRE: m >= n > 0
int gcd( int m, int n ) {
int tmp;
while ( m%n > 0 ) {
tmp = n;
n = m%n;
m = tmp;
}
return n;
} |
|
|
| Den rekursive er en anelse enklere, men forskellen er igen ubetydelig.
|
|
|
2.4 Eksponentiering
|
|
| Vi vil her udnytte følgende formel til at beregne xy på
en hurtig måde:
|
|
|
|
|
| Hvis vi f.eks. vil beregne 28, kan vi udnytte at 28
= 24 * 24, og 24 = 22 * 22,
og 22 = 21 * 21 = 2 * 2 = 4. Hvis vi
indsætter den anden vej får vi 24 = 4 * 4 = 16, og 28
= 16 * 16 = 256.
|
|
| Man skal bemærker, at vi kun har udført 3 multiplikationer, i modsætning
til den traditionelle metode: 28 = 2 * 2 * 2 * 2 * 2 * 2 *
2 * 2 = 256, med 7 multiplikationer.
|
|
| Hvis vi giver xy den funktionelle betegnelse power( x, y )
kan vi formulere denne teknik rekursivt:
|
|
|
|
power( x, y ) = power( x, y/2 ) * power( x, y/2 ), y er lige
power( x, y ) = power( x, y/2 ) * power( x, y/2 ) * x, hvis y er ulige
power( x, 0 ) = 1 |
|
|
| hvis y ikke er negativ.
|
|
|
Den sidste formel ganger x på, hvis y er ulige. Det skyldes, at der
bliver én til rest i forhold til de to y/2'er når y er ulige.
|
|
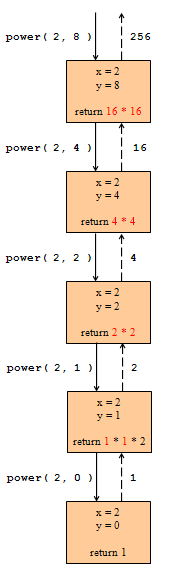
| Hvis vi igen ser eksemplet med 28, vil det rekursive forløb blive
|
Figur 4:
Forløbet af de rekursive kald
|
|
|
| Ud fra definitionen skulle man tro at det rekursive forløb ville være
et træ, da der er to rekursive kald. Disse to kald er dog ens, hvorfor
man kun udfører det ene og genbruger resultatet.
|
|
| Den rekursive metode bliver:
|
Source 8:
Rekursiv: Exponen-tiering
|
for ( int i=0; i<=10; i++ )
print( power( 2, i ) + " " );
println();
// PRE: y>=0
int power( int x, int y ) {
if ( y==0 )
return 1;
else {
int halvPower = power( x, y/2 );
int fuldPower = halvPower * halvPower;
if ( y%2 == 1 )
fuldPower *= x;
return fuldPower;
}
} |
1 2 4 8 16 32 64 128 256 512 1024
|
|
|
|
2.5 Skabelon for matematisk rekursion
|
|
|
Man kan opstille en generel skabelon, som stort set alle matematisk
rekursive metoder kan opbygges efter:
|
Pseudo 3:
Matematisk rekursion
|
// PRE: n er okay
int rekursiv( int n ) {
if ( n er basis )
// basis - én eller flere mulige værdier
else
// rekursions skridt - ét eller flere rekursive kald
} |
|
|
|
Man bemærker at basis godt kan bestå af flere værdier (som i fibonacci
eksemplet), hvilket blot kræver flere else-if'er.
|
|
|
3. Andre eksempler
|
|
|
3.1 Palindrom
|
|
|
Palindromer er ord der staves ens forfra og bagfra. F.eks. MELLEM og
REJER. Det problem vi vil se på, er at fastslå om et givet ord er et
palindrom. Vores metode vil derfor have signaturen:
|
|
|
boolean palindrom( String ord ) |
|
| Sætte samme bogstav udenom
|
Umiddelbart kan det være lidt vanskeligt at se hvad der skal være det
rekursive skridt, men så kan man modsat starte med at identificere basis.
En tom streng er et palindrom, og en streng med ét tegn er også et palindrom,
men hvad så. Hvis man skal udvide en streng der er et palindrom så det
vedbliver med at være et palindrom, kan man gøre det ved at sætte det
samme bogstav udenom. Hvis vi f.eks. havde ELLE og ville udvide det,
så kunne vi placere det samme bogstav M på begge sider og få MELLEM.
Da man i rekursion arbejder sig frem mod basis, vil processen derimod
blive den omvendte: at man fjerner de to yderste bogstaver, så man går
fra MELLEM, til ELLE, til LL, til den tomme streng. Man skal så hele
tiden kontrollere at de to bogstaver man fjerner er ens, ellers er det
ikke et palindrom.
|
|
|
Vores rekursive definition på et palindrom bliver:
|
|
|
|
S0S1 ... Sn-1Sn er
et palindrom hvis S0 er det samme bogstav som Sn
og S1 ... Sn-1 er et palindrom
S0 er et palindrom og den tomme streng er et palindrom |
|
|
|
hvor vi angiver strengene som sekvenser af tegn Si.
|
|
|
Den rekursive metode bliver derfor:
|
Source 9:
Rekursiv: Palindrom
|
boolean palindrom( String ord ) {
if ( ord.length() < 2 )
return true;
else if ( ord.charAt( 0 ) == ord.charAt( ord.length() - 1 ) )
return palindrom( ord.substring( 1, ord.length() - 1 ) );
else
return false;
} |
|
| Frem mod terminering
|
Det der her driver rekursionen frem mod terminering er naturligvis
at den tekststreng vi skal kontrollere bliver stadig mindre. Man bemærker
også at den tunede effekt af &&
stopper rekursionen første gang to tegn ikke er ens, ellers ville rekursionen
altid nå basis.
|
|
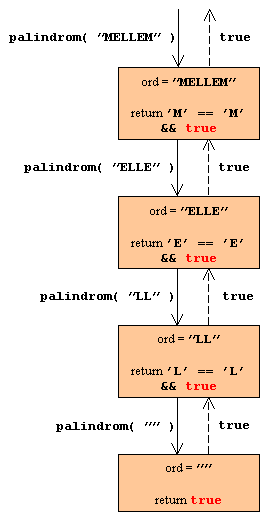
| Hvis vi ser på kaldet: palindrom(
"MELLEM" ), bliver forløbet som følger:
|
Figur 5:
Forløbet af de rekursive kald
|
|
|
| Her er der tale om et palindrom og man observerer derfor at kaldene
når helt ned til basis, der i dette tilfælde er den tomme streng.
|
|
| Lad os se en iterativ løsning:
|
Source 10:
Iterativ: Palindrom
|
boolean palindrom( String ord ) {
for ( int pos=0; pos < ord.length(); pos++ )
if ( ord.charAt( pos ) != ord.charAt( ord.length - 1 - pos ) )
return false;
return true;
} |
|
|
| Igen er der ikke den store forskel i løsningernes omfang.
|
|
|
3.2 Towers of Hanoi
|
|
| Towers of Hanoi er konge-eksemplet i rekursion. Når man først ser og
forstår Towers of Hanoi vil man blive imponeret over hvor utrolig enkelt,
et ellers meget uoverskueligt problem kan løses. Det er et af de mest
kraftfulde af sin art.
|
| "Der var engang ..."
|
Et sted i østen er der et munkekloster. I dette kloster
befinder der sig en mærkelig opstilling. På tre pinde af guld er der
placeret 64 skiver ligeledes af guld. Alle skiverne har forskellig diameter,
og sidder på pindene gennem et hul i deres centrum. Ved verdens begyndelse
anbragte en guddom de 64 skiver på den ene pind, på en sådan måde at
ingen skive lå ovenpå en mindre skive - de lå som en pyramide! Munkene
fik nu til opgave at flytte skiverne over på en af de andre pinde. Der
var dog nogle strenge regler for hvordan dette skulle gå for sig. De
måtte kun flytte en skive af gangen, og de måtte aldrig placere en større
skive oven på en mindre. Når munkene havde fundført deres opgave ville
verden gå under! Man skal dog ikke være så bekymret over det. For ca.
1000 år siden opstod der en religiøs strid om hvilken af de to andre
pinde den endelige pyramide skal være på. Der er endog en tredie fraktion
der mener at de to andre modarbejder det hele, da det de betragter som
startpinden af disse regnes for at være slutpinden. Da de tre fraktioner
af politiske grunde er blevet nød til at dele arbejde mellem sig, forventes
de ikke at blive færdige før De kære læser for længst har lært at programmere!
|
|
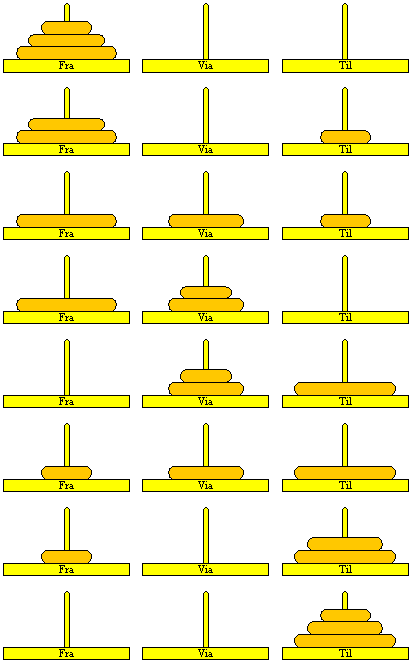
| Se, det med 64 skiver af guld, det var der ikke rigtig råd til, og
det tager jo også så forfærdelig lang tid - så vi nøjes lige med tre skiver
i første omgang:
|
Figur 6:
Towers of Hanoi med tre skiver
|
|
|
| Med tre skiver er det rimelig nemt at kombinere sig frem til en løsning.
Syv gange flytter vi en skive. Man observerer at den største skive flyttes
som den midterste flytning og at det først kan lade sig gøre når alle
de andre er på den midterste pind.
|
|
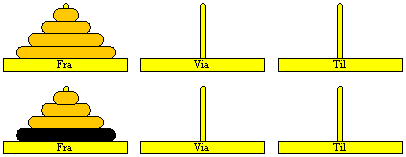
| Lad os bruge denne observation til at løse problemet med 4 skiver:
|
Figur 7:
Del-problem med tre skiver
|
|
|
| Først skiller vi rent visuelt den største skive ud. Dermed er problemet
for en stund reduceret til at flytte de tre øverste skiver til den midterste
pind.
|
|
| At flytte de tre skiver gøres ved at bruge løsningen fra før; hvor
vi i stedet flytter til den midterste via den højre
|
Figur 8:
Løsning af del-problem med tre skiver
|
|
|
| Dernæst skal den store skive flyttes:
|
Figur 9:
Flytning af den store skive
|
|
|
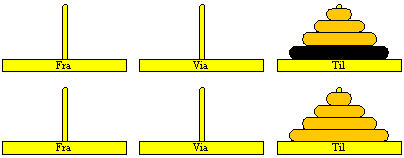
| Endelig er der så opgaven med at flytte de tre skiver fra pinden i
midten over på den store skive, men det er jo det samme del-problem som
før.
|
|
| En tur via pinden til venstre giver derfor:
|
Figur 10:
Løsning af del-problem med tre skiver
|
|
|
| Det rekursive i løsningen begynder nu at tegne sig. Hvis vi kan løse
problemet med tre skiver kan vi også løse det med fire skiver. Vi gør
det ved først at løse et del-problem med tre skiver, dernæst flytte én
skive og igen løse et del-problem med tre skiver.
|
|
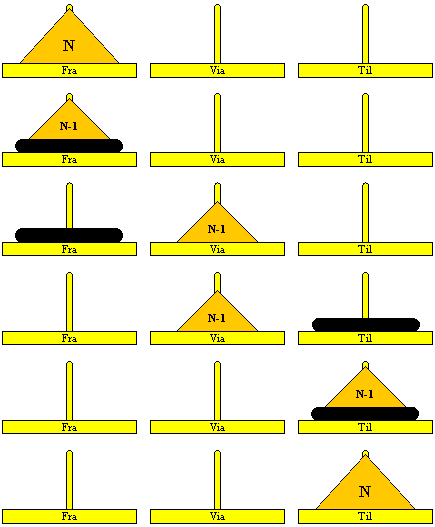
| Lad os generalisere det til N skiver, med to del-problemer med N-1
skiver:
|
Figur 11:
Løsning af problem med N skiver, ved løsning af to del-problemer med
N-1 skiver
|
|
|
| Når vi skal lave et program der løser dette problem vha. rekursion
er spørgsmålet mere præcist: Hvad er en løsning? Hvad skal programmet
skrive ud?
|
|
| Det der skal specificeres, er hvilke flytninger der skal foretages.
|
|
|
Towers of Hanoi bliver som følger:
|
Source 11:
Rekursiv: Towers of Hanoi
|
int nSkiver = 3;
hanoi( nSkiver, 1, 3, 2 );
void hanoi( int antal, int fra, int til, int via ) {
if ( antal > 1 ) {
hanoi( antal-1, fra, via, til );
println( fra + " -> " + til );
hanoi( antal-1, via, til, fra );
} else
println( fra + " -> " + til );
} |
1 -> 3
1 -> 2
3 -> 2
1 -> 3
2 -> 1
2 -> 3
1 -> 3 |
|
|
| Hvad så med en iterativ løsning? Den ligger det faktisk temlig tungt
med!
|
| Stakke
| Vi skal senere, når vi studerer den datastruktur der kaldes stakke,
se hvordan man altid kan implementere rekursion iterativt vha. en stak,
og dét er nødvendigt, hvis vi vil lave Towers of Hanoi iterativt.
|
|
|
4. Adapter-metode
|
|
| Betragt følgende rekursive metode:
|
Source 12:
Rekursiv: Udskriv array
|
int[] t = { 5, 8, 9, 3, 6, 5, 4, 1 };
udskrivArray( t, 0 );
void udskrivArray( int[] tabel, int pos ) {
if ( pos < tabel.length ) {
print( tabel[ pos ] + " " );
udskrivArray( tabel, pos + 1 );
}
if ( pos == 0 )
println();
} |
|
| Nødvendigt at hjælpe metoden
| Det man skal bemærke er det grimme kald. Man er altid nød til at sætte
den i gang med den første værdi for pos,
nemlig 0. Samtidig er
det grimt at den rekursive metode skal have en ekstra if-sætning for at
kunne afslutte med et linieskift når den er færdig med udskriften. Den
if-sætning bliver slæbt med igennem hele forløbet selv om den altid
kun blive udført af den første metode-kopi. Det ville være at foretrække
at placere println()
efter kaldet i anden linie,
men så er der endnu mere man skal hjælpe metoden med.
|
|
| For at slippe af med disse upraktiske krav til den der kalder metoden
bruger man normalt en adapter-metode [FKJ]. Adapter-metoden bruger
overloading til at lægge sig mellem den rekursive metode og den der ønsker
at kalde den. Adapter-metoden yder den rekursive metoden den hjælp den
behøver.
|
|
| Med en sådan overloading bliver vores program:
|
Source 13:
Rekursiv: Udskriv array, med adapter metode
|
int[] t = { 5, 8, 9, 3, 6, 5, 4, 1 };
udskrivArray( t );
void udskrivArray( int[] tabel, int pos ) {
if ( pos < tabel.length ) {
print( tabel[ pos ] + " " );
udskrivArray( tabel, pos+1 );
}
}
void udskrivArray( int[] tabel ) {
udskrivArray( tabel, 0 );
println();
} |
|
|
| Vi kan nu tilbyde en metode der blot skal kaldes, med de nødvendige
oplysninger og ikke mere.
|
|
| Man kan en sjælden gang komme ud for at adapter-metoden og den rekursive
metode har samme signatur. I så flad må man opgive at overloade og i stedet
ændre navnet på den rekursive metode, så adapter-metoden får det "rigtige"
navn.
|
|
|
5. Hale-rekursion
|
|
| En bestemt gruppe af rekursive metoder kaldes "hale-rekursive":
|
|
|
|
Definition: Hale-rekursiv metode
En rekursiv metode er hale-rekursiv, hvis den
højest kalder sig selv én gang, og dette kald er det
sidste der udføres før metoden returnerer. |
|
|
| Lad os se hvilke af de eksempler vi har gennemgået, der er hale-rekursive.
|
|
| Først er der eksemplet med Ikast Svømmehal. Det afsluttes med et kald
af checkBassin, og da
det ligeledes er det eneste kald er metoden hale-rekursiv.
|
|
| Fakultet, største fælles divisor og palindrom er på samme måde hale-rekursive.
|
|
| Fibonacci og Towers of Hanoi er ikke hale-rekursive. For begge gælder
der, at der er mere end et rekursivt kald.
|
|
| Hale-rekursion - hvad kan man så bruge det til?
|
| Bør omformes til iterativ
| Hvis en metode er hale-rekursiv er det rimelig enkelt at omforme den
til en iterativ løsning. Så enkelt at man reelt altid bør foretrække at
gøre det. Selve argumentet for at foretrække en iterativ løsning frem
for en rekusiv, såfremt de er lige enkle at implementere, vender vi tilbage
til i næste afsnit.
|
|
| En hale-rekursiv metode vil normalt have følgende opbygning:
|
Pseudo 4:
Hale-rekusion
|
// PRE: parametre er okay
... haleRekursion( ... ) {
if ( <ikke basis> ) {
<udfør rekursions-skridt>;
haleRekursion( ... );
} else {
// basis
...
}
} |
|
|
| Der generelt kan omformes til:
|
Pseudo 5:
Iterativ udgave af Hale-rekusion
|
// PRE: parametre er okay
... haleRekursion( ... ) {
...
while ( <ikke basis> ) {
<udfør rekusions-skridt>;
}
...
} |
|
| if og while
| Det kan være lidt forskelligt hvordan det konkret skal laves, bla.
mht. hvordan basis skal håndteres. Dog er udskiftningen af if
med while meget karakteristisk
for alle omformninger af rekursive løsninger til iterative.
|
|
|
6. Rekursion eller iteration
|
|
| Hvad skal man så bruge: Rekursion eller iteration?
|
|
| Spørgsmålet er naturligvis hvilken løsning der i det konkrete tilfælde
er den bedste, men hvad vil det i den sammenhæng sige at være bedst?
|
|
| Her kan vi se på nogle af de mål, fra kapitlet om programmeringssprog,
der kommer ind i billedet.
|
|
|
| Det skal være let at formulere løsningen |
Det kommer naturligvis an på det konkrete problem man løser.
I første række falder det tilbage på om problemet viser sine rekursive
eller iterative egenskaber. Dette afhænger ofte af øjet der ser.
Som vi senere skal se, i kapitlet om stakke, kan man altid implementere
en rekursiv løsning iterativt, men det gør det aldrig lettere
at formulere den. |
| Det skal være let at forstå løsningen
| Her forudsættes naturligvis at den der læser forstår rekursion.
Rekursive løsninger er ofte lettere at læse end iterative. Det er
sjældent omvendt. I de fleste tilfælde kan det være det samme, såfremt
de udviser samme enkelthed.
|
| Løsningen skal være hurtig
| Hvad er hurtigst? Generelt er iteration klart hurtigere end rekursion.
Det skyldes at metode-kald tager ekstra tid at udføre. |
|
|
| Som man ser, ligger rekursionens primære styrke i formuleringen af
løsningen. Hvis man af effektivitetsgrunde insisterer på en iterativ løsninger
kan man altid få det.
|
|
|
|
Konklusion:
Man skal benytte rekursion i stedet for iteration,
såfremt:
- Den rekursive løsning er enklere at formulere/forstå
- Det ikke giver effektivitetsproblemer
|
|
|
|
Repetitionsspørgsmål
|
| 1
| Hvilken sammenhæng er der mellem rekursion og nedbrydning?
|
| 2
| Hvad er en rekursiv metode?
|
| 3
| Hvad er et rekursions-skridt?
|
| 4
| Hvad er rekursions-basis?
|
| 5
| Hvad er rekursions-skridt og -basis i fakultet eksemplet?
|
| 6
| Hvad er rekursions-skridt og -basis for fibonacci talrækken?
|
| 7
| Hvad menes der med "spildte metode-kald" i fibonacci eksemplet?
|
| 8
| Hvordan optimeres den iterative udgave af fibonacci-metoden?
|
| 9
| Hvad er rekursions-skridt og -basis i eksemplet med Euclids algoritme,
til at finde største fælles divisor?
|
| 10
| Hvad er et palindrom?
|
| 11
| Hvad er rekursions-skridtet og -basis i palindrom eksemplet?
|
| 12
| Hvorfor bruger man i nogle situationer en adapter-metode?
|
| 13
| Hvad er en hale-rekursiv metode?
|
| 14
| Giv et eksempel på en hale-rekursiv metode og forklar?
|
| 15
| Hvad interessant er der ved hale-rekursion?
|
| 16
| Hvilket forhold er der mellem if og while i forbindelse med rekursion
og iteration?
|
| 17
| Hvornår skal man anvende rekursion i stedet for iteration?
|
|
|
Svar på repetitionsspørgsmål
|
| 1
| Rekursion laves ved en meget skæv nedbrydning. Man deler i to del-problemer:
Et lille der umiddelbart kan løses og et større der er af samme slags
som det oprindelige problem.
|
| 2
| En metode der kalder sig selv.
|
| 3
| Det er opdeling af problemet, løsning af det lille del-problem.samt
vidersendelse af det resterende problem ved et eller flere rekursive kald.
|
| 4
| Det resterende problem, når det selv når et omfang der umiddelbart
kan løses.
|
| 5
| Skridtet er at man ganger det tal man er nået til med resten af løsningen.
Basis er 0 der giver 1.
|
| 6
| Skridtet er at man lægger de to foregående tal sammen. Basis i talrækken
er 0 og 1 (man lader nogle gange basis være 1 og 1).
|
| 7
| Metode-kald der alle har samme aktuelle parameter. I princippet burde
kun en af dem være nødvendig.
|
| 8
| Ved at flytte basis, så man i stedet beregner den oprindelige basis.
|
| 9
| Skridtet er, at man finder den største fælles divisor for to tal, som
den største fælles divisor af den mindste af tallene, og den største modulus
den mindste. Basis er, at den mindste går op i den største (dvs. at førnævnte
modulus giver 0).
|
| 10
| Et palindrom er et ord der staves ens forfra og bagfra.
|
| 11
| Skridtet er, at man sammenligner og fjerner det første og sidste tegn
i ordet. Basis er enten den tomme streng eller strengen med længde 1.
I begge tilfælde angiver basis, at der er tale om et palindrom.
|
| 12
| Fordi den rekusive metode kan have brug for lidt "hjælp",
der ikke bør vedkomme den der kalder metoden.
|
| 13
| En metode der højest foretager ét rekursivt kald og dette i
så fald er det sidste der sker før metoden returnerer.
|
| 14
| Den rekursive metode i palindrom eksemplet er hale-rekusiv fordi den
kun har et rekusivt kald og dette er placeret som det sidste før der returneres.
|
| 15
| Hale-rekursion kan altid ellimineres uden at man er nød til at simulere
rekursion.
|
| 16
| if udskiftes typisk med while i forbindelse med, at man omformer en
rekursiv metode til en iterativ.
|
| 17
| Når det giver en enklere løsning, der er lettere at læse/formulere,
og det samtidig ikke giver effektivitetsproblemer.
|